The Quantum Adversary:

Lower bounds for both classical and quantum algorithms have been attained in the past by analyzing the behavior of the algorithm in the face of an adversary. Ambainis uses a quantum adversary as the basis for his lower bound theorem; instead of running a quantum algorithm against one input, it is run against a superposition of inputs. The formulation of the quantum adversary and the justification for why a lower bound in the quantum adversary model is also a lower bound in the standard oracle query model below are adapted and somewhat simplified from Ambainis' paper [1].

Ambainis observed that any standard oracle query algorithm A that operates only on a single input is also correct in the quantum adversary model. Consider a standard oracle query algorithm A that uses T queries and succeeds with probability p. We assume our quantum memory register begins in the $\left\vert\vphantom{ 0 }\right.$ 0$\left.\vphantom{ 0 }\right\rangle$ state. For every input x $\in$ {0, 1}^N, the algorithm transforms the initial state $\left\vert\vphantom{ 0 }\right.$ 0$\left.\vphantom{ 0 }\right\rangle$ $\otimes$ $\left\vert\vphantom{ x }\right.$x$\left.\vphantom{ x }\right\rangle$ into the final state

$$\left(\vphantom{ \alpha_{x}\left\vert f(x)\right\rangle + \beta_{x}\vert\overline{f(x)}\rangle }\right.$$$$\alpha_{{x}}^{}$$$$\left\vert\vphantom{f(x)}\right.$$f (x)$$\left.\vphantom{f(x)}\right\rangle$$ + $$\beta_{{x}}^{}$$|$$\overline{{f(x)}}$$$$\rangle$$$$\left.\vphantom{ \alpha_{x}\left\vert f(x)\right\rangle + \beta_{x}\vert\overline{f(x)}\rangle }\right)$$ $$\otimes$$ $$\left\vert\vphantom{w_{x}}\right.$$w_x$$\left.\vphantom{w_{x}}\right\rangle$$ $$\otimes$$ $$\left\vert\vphantom{x}\right.$$x$$\left.\vphantom{x}\right\rangle$$

where |$\alpha_{{x}}^{}$|² + |$\beta_{{x}}^{}$|² = 1, and |$\alpha_{{x}}^{}$|²$\ge$p (so |$\beta_{{x}}^{}$|²$\le$1 - p, and finally | w_x$\rangle$ is the remaining state of the memory. The same algorithm will take any superposed input state

| 0$$\rangle$$ $$\otimes$$ $$\sum_{{x \in S}}^{}$$$${\frac{{1}}{{\sqrt{\left\vert S\right\vert}}}}$$$$\left\vert\vphantom{x}\right.$$x$$\left.\vphantom{x}\right\rangle$$

to the final state

$${\frac{{1}}{{\sqrt{\vert S\vert}}}}$$$$\sum_{{x \in S}}^{}$$$$\left(\vphantom{ \alpha_{x}\left\vert f(x)\right\rangle + \beta_{x}\vert\overline{f(x)}\rangle }\right.$$$$\alpha_{{x}}^{}$$$$\left\vert\vphantom{f(x)}\right.$$f (x)$$\left.\vphantom{f(x)}\right\rangle$$ + $$\beta_{{x}}^{}$$|$$\overline{{f(x)}}$$$$\rangle$$$$\left.\vphantom{ \alpha_{x}\left\vert f(x)\right\rangle + \beta_{x}\vert\overline{f(x)}\rangle }\right)$$ $$\otimes$$ $$\left\vert\vphantom{w_{x}}\right.$$w_x$$\left.\vphantom{w_{x}}\right\rangle$$ $$\otimes$$ $$\left\vert\vphantom{x}\right.$$x$$\left.\vphantom{x}\right\rangle$$.

Note that in this end state, if the oracle is measured to be x, a measurement of the memory register will yield f (x) with probability |$\alpha_{{x}}^{}$|²$\ge$p. Ambainis places a lower bound on the number of oracle queries required by any quantum adversary algorithm to produce such an end state from such a start state.

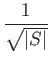
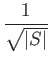
This argument gives us a lower bound in the standard oracle query model as well. If T queries are required of a quantum adversary algorithm to establish a correct end state with probability p, then no standard oracle query algorithm A can compute f with bounded probability p in t < T queries.

This quantum adversary method provides a framework for proving a great diversity of lower bounds. Indeed, nearly every lower bound in this thesis is proved directly or indirectly using Theorem 2.1.1. As useful as the theorem is, it does have limitations, one of which is discussed in Section 2.4.