


Next: Corollary 1.2
Up: Proof that Algorithm Increases
Previous: Theorem 1
Contents
Corollary 1.1: We seek to show that after applying A, both k'
and l' are positive, under the following conditions:
Let the state vector for:
- one state have amplitude k
- each of the remaining (N - 1) states the amplitude is l
And let:
- k and l be real
- k be negative, and l be positive
-
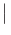
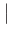 <
< 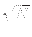
- N
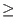 9
9
Then, after applying A, both k' and l' are positive.
Proof:
First we will show that k' is positive:
Next we will show that l' is positive:
[Grover96]



Next: Corollary 1.2
Up: Proof that Algorithm Increases
Previous: Theorem 1
Contents
Matthew Hayward - Quantum Computing and Grover's Algorithm GitHub Repository
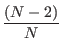 l >
l > 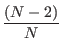 l >
l >