


Next: Corollary 1.1
Up: Proof that Algorithm Increases
Previous: Proof that Algorithm Increases
Contents
Theorem 1: Given the state vector of our register with one state with
amplitude k, and every other state with amplitude l, after an
application of A:
- the amplitude in the one state is
k' =
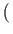
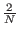 - 1
- 1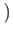 k + 2
k + 2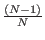 l
l
- the amplitude of the remaining (N - 1) states is
l' =
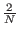 k +
k + 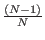 l
l
Proof: Given the definition of A as
Aij = 2/N if
i 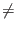 j
and
Aii = - 1 + 2/N, it follows from the definition of matrix
multiplication of k and l by A that:
j
and
Aii = - 1 + 2/N, it follows from the definition of matrix
multiplication of k and l by A that:
-
k' =
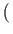
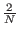 - 1
- 1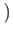 k + 2
k + 2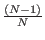 l
l
-
l' =
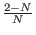 l +
l + 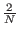 k +
k + 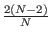 l
l
The second expression simplifies to
l' = 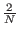 k +
k + 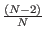 l with some simple algebraic
manipulation. [Grover96]
l with some simple algebraic
manipulation. [Grover96]



Next: Corollary 1.1
Up: Proof that Algorithm Increases
Previous: Proof that Algorithm Increases
Contents
Matthew Hayward - Quantum Computing and Grover's Algorithm GitHub Repository
![]() j
and
Aii = - 1 + 2/N, it follows from the definition of matrix
multiplication of k and l by A that:
j
and
Aii = - 1 + 2/N, it follows from the definition of matrix
multiplication of k and l by A that: