A Formal Description of a Quantum Register

The state of any quantum mechanical system is described by a state vector in an appropriate Hilbert space. A Hilbert space is a complex linear vector space. [Greenwood00] This is similar to more familiar vector spaces with the exception that vectors may have complex lengths. A linear vector space is one in which the sum or constant multiple of a vector within the space is within the space as well. [Griffiths95]

In the case of our n bit quantum register, our Hilbert space will be of dimension 2ⁿ. The orthogonal basis for the Hilbert space can be conveniently chosen to be the 2ⁿ possible basis states that the quantum register can be found in when measured.

With the chosen basis, the projection of the state vector on the i'th basis vector will be the amplitude of the portion of the wave function corresponding to the register being solely in the i'th state.

The state vector can be written $\Psi$ = (a₁, a₂,...a_N)^T, where N = 2ⁿ. a_i is the amplitude of the wave function in the i'th state, or equivalently the projection of the state vector onto the i'th basis state. The probability of measuring the register in the i'th state is then:

$${\frac{{\vert a_{i}\vert^{2}}}{{\sum_{j = 1}^{N}\vert a_{j}\vert^{2}}}}$$

where | c|² = c^*c, here * is the complex conjugate operator, so if c = a + b$\sqrt{{-1}}$, | c|² = a² + b². [WC98] In general the amplitude of any component of the wave function may be complex, but Grover's algorithm itself does not use any complex amplitudes.

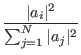
If we we insist that

$$\sum_{{j = 1}}^{{N}}$$| a_j|² = 1

then the probability of measuring the register to be in the i'th state becomes simply | a_i|², where a_i is the i'th component of the state vector. In this case we say the vector is normalized.

In the absence of measurement the state vector of any quantum system, including our quantum register, will evolve according to the Schrödinger wave equation. The Schrödinger equation has the property that if the solution is normalized at any time, it is normalized at all times. [Griffiths95] Therefore if we initialize our quantum register to be normalized, we can be sure that at all future times the probability of measuring the quantum register in the i'th state will be given simply by | a_i|².

A consequence of the Schrödinger equation is that the evolution of the system must be reversible. At any point in time, if we know the solution to Schrödinger's equation, we can derive its solution at all past and future times. Thus any transformation we wish to perform on our system should be reversible. For our quantum register this means that for any operation we use, we must be able to say what the state of the register was before the operation, given the operation and the resulting state. [Grover00] These remarks apply only to quantum systems evolving in isolation of their environment. Any measurement of the register will irreversibly alter the system, collapsing its wave function into one of its base states.