Application to Generalized XOR

To see how simple proofs can be with Lemma 2.2.1 we provide an example. Generalized XOR is the N-bit Boolean function that is 0 if and only if its input bits are all the same.

Theorem 2.2.1   $\Omega$($\sqrt{{N}}$) oracle queries are required to compute the generalized XOR of N bits in the bounded error setting.

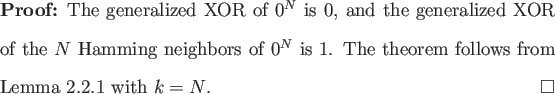
This lower bound is asymptotically tight: Beals et al. provide O($\sqrt{{N}}$) oracle query algorithms for computing the AND or OR of N bits in the bounded error setting [2], and the generalized XOR of N bits is just $\overline{{AND \vee \overline{OR}}}$. Unfortunately, Ambainis' Theorem does not always perform this well, as we demonstrate in the next two sections.