


Next: Superposition
Up: State Vectors and Dirac
Previous: State Vectors:
Contents
The standard notation for a state vector is a ket vector
|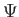
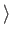 . For example, a vector in
. For example, a vector in 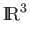 with basis
with basis
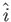 ,
,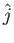 ,
,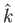 is typically written as
is typically written as
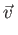
=
a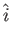
+
b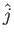
+
c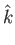
= (
a,
b,
c)
T.
In Dirac notation, it would be written as
|
v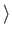
=
a|
i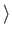
+
b|
j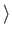
+
c|
k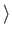
= (
a,
b,
c)
T.
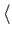 y|. The inner product of a bra and a ket
vector is written
y|. The inner product of a bra and a ket
vector is written
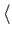 y| x
y| x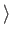 , and is called a bracket
[18].
, and is called a bracket
[18].



Next: Superposition
Up: State Vectors and Dirac
Previous: State Vectors:
Contents
Matthew Hayward Lower Query Bounds in the Quantum Oracle Model GitHub Repository
![]()
![]() . For example, a vector in
. For example, a vector in ![]() with basis
with basis
![]() ,
,![]() ,
,![]() is typically written as
is typically written as