Vector Mathematics

The only operations that are used in Shor's algorithm on vectors are addition, length determination, and scaling. The vector in question is that state vector of a quantum mechanical system, it is a complex vector in a Hilbert Space.

For example, a n state quantum system requires a n dimensional Hilbert Space to represent its state vector. The quantum system can be measured in any of the n states, and to represent this we imagine each of the n states as mutually perpendicular axes within a Hilbert space. Thus the state vector for a system in the j'th state is equal to:

$$\left(\vphantom{ \begin{array}{c} 0 \\ 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \end{array} }\right.$$$$\begin{array}{c} 0 \\ 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \end{array}$$$$\left.\vphantom{ \begin{array}{c} 0 \\ 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \end{array} }\right)$$

For the n states, where the number at the top of the column is the length of the state vector projected onto the 1st state, and the 1 appears in the j'th row.

To add two vectors we simply add their components.

$$\left(\vphantom{ \begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array} }\right.$$$$\begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array}$$$$\left.\vphantom{ \begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array} }\right)$$ + $$\left(\vphantom{ \begin{array}{c} b_{1} \ b_{2} \ b_{3} \end{array} }\right.$$$$\begin{array}{c} b_{1} \ b_{2} \ b_{3} \end{array}$$$$\left.\vphantom{ \begin{array}{c} b_{1} \ b_{2} \ b_{3} \end{array} }\right)$$ = $$\left(\vphantom{ \begin{array}{r} a_{1}+b_{1} \ a_{2}+b_{2} \ a_{3}+b_{3} \end{array} }\right.$$$$\begin{array}{r} a_{1}+b_{1} \ a_{2}+b_{2} \ a_{3}+b_{3} \end{array}$$$$\left.\vphantom{ \begin{array}{r} a_{1}+b_{1} \ a_{2}+b_{2} \ a_{3}+b_{3} \end{array} }\right)$$

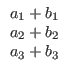
Since this vector lies in a Hilbert Space the projections of the state vector onto the coordinate axes are allowed to be complex numbers, thus the definition of length is slightly different from what is expected.

The length of a vector in a Hilbert space with n components is defined to be: $\sqrt{{\sum_{j = 1}^{n}\vert w_{j}\vert^{2}}}$ where w_j is the value of the j'th component of the vector, and | w_j|² is defined to be w_j times its complex conjugate, or when w_j = a + i*b, | w_j|² = a² + b² . To scale a vector by any length l you simply multiply each component of the vector by the value l. In particular to scare a vector to length 1 you multiply each component by the inverse length of the vector.