next up previous contents
Next: Conclusion Up: Quantum Computing, Shor's Algorithm, Previous: Parallelizing Methodology   Contents

Timing Results and speedup

Even given the small amount of code that was parallelized, we got remarkably good speedup results.

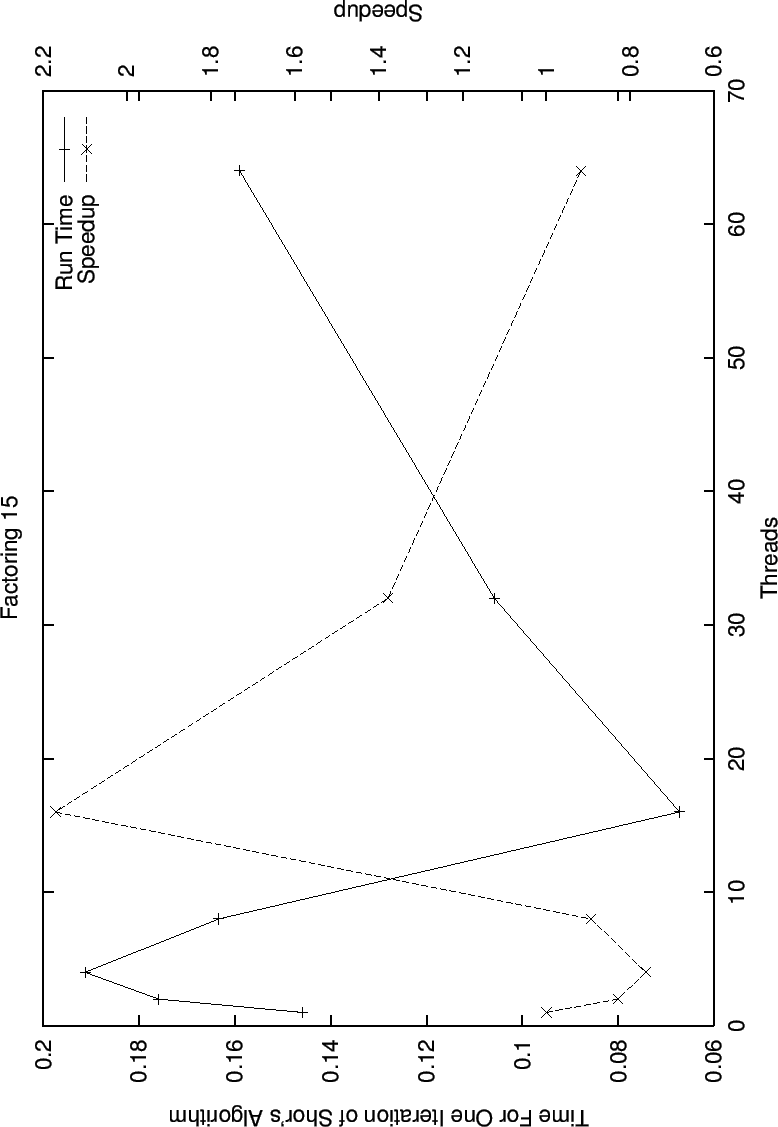
As can be seen, there is not a strong correlation between number of processors and run time for the trials factoring 15 (4 bits), although this can be accounted for by the fact that the run time is so small initially, and for all number of threads the run time is less than one fifth of a second. This will change rapidly, as the running time grows exponentially with n, the number to be factored.

Figure 1: Run Times and Speedups for Simulation of Shor's Algorithm Factoring 15
\begin{figure}\epsfig{figure=15.epsi}\end{figure}

In this graph for the factoring of 21 (5 bits), we begin to see possible speedup due to multiple threads, although it is still sporadic, again, this is not surprising due to the very small running times of the sequential version.

Figure 2: Run Times and Speedups for Simulation of Shor's Algorithm Factoring 21
\begin{figure}\epsfig{figure=21.epsi}\end{figure}

In this graph for running times and speedups while factoring 33 (6 bits), we see the beginning of our linear speedup with the number of pthreads. With the exception of the speedup for two threads, we follow a roughly liner speedup curve.

Figure 3: Run Times and Speedups for Simulation of Shor's Algorithm Factoring 33
\begin{figure}\epsfig{figure=33.epsi}\end{figure}

In the graph for the speedup with thread increase while factoring 77 (7 bits) we see even better behavior than we did for factoring 33. There is initially linear speedup, but once the run time gets sufficiently small, the speedup drops off, here we can see the results of the sequential time becoming the dominant portion of the running time.

Figure 4: Run Times and Speedups for Simulation of Shor's Algorithm Factoring 77
\begin{figure}\epsfig{figure=77.epsi}\end{figure}

In the graph for speedup and decrease run time while factoring 221 (8 bits) we see super linear speedup, which is as good as we can possibly hope for.

Figure 5: Run Times and Speedups for Simulation of Shor's Algorithm Factoring 221
\begin{figure}\epsfig{figure=221.epsi}\end{figure}

In the graph of speedup while factoring 391 (9 bits), we see that the good behavior while factoring 221 continues. At this point the exponential slowdown made it difficult to continue gathering speedup data for larger numbers.

Figure 6: Run Times and Speedups for Simulation of Shor's Algorithm Factoring 391
\begin{figure}\epsfig{figure=391.epsi}\end{figure}

next up previous contents
Next: Conclusion Up: Quantum Computing, Shor's Algorithm, Previous: Parallelizing Methodology   Contents
Matthew Hayward - Quantum Computing, Shor's Algorithm, and Parallelism GitHub Repository