Probability Interpretation

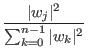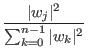
Now that we know how to represent a state vector as a superposition of states, and yet can only measure the state vector to be in one of the base states. We must determine what happens when we measure the state vector.

The only way to observe the state of the state vector is to in some way cause the quantum mechanical system to interact with the environment. When the state vector is observed it makes a sudden discontinuous jump to one of the eigenstates. (Williams, Clearwater)

To perform any sort of useful calculation we must be able so say something about which base state a quantum mechanical system will collapse into. The probability that the state vector will collapse into the j'th eigenstate, is given by | w_j|² which is defined to be a_j² + b_j² if w_j = a_j + i*b_j, where w_j is the complex projection of the state vector onto the j'th eigenstate. In general the chance of choosing any given state is

Prob(j) = $${\frac{{\vert w_{j}\vert^{2}}}{{\sum_{k = 0}^{ n-1} \vert w_{k}\vert^{2}}}}$$

but as mentioned earlier we will insist on having the state vector of length one, and in this case the probability expression simplifies to Prob(j) = | w_j|².