Nonconstant Symmetric Functions

AND, OR, MAJORITY, and PARITY are all symmetric functions, and the lower bounds attained in the preceding section are all asymptotically tight. Our success leads us to investigate what we can prove about symmetric functions in general.

Theorem 2.7.1   $\Omega$($\sqrt{{N}}$) oracle queries are required to compute any N-bit nonconstant symmetric Boolean function in the bounded error setting.

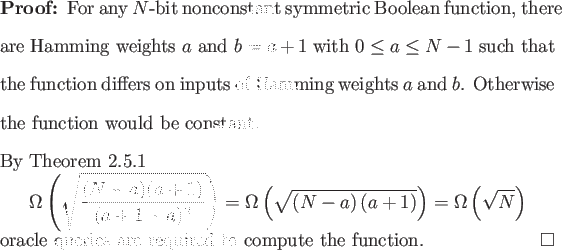
Depending on the value of a in Theorem 2.7.1 we may be able to provide a better lower bound than $\Omega$($\sqrt{{N}}$). This result was previously established by Beals et al. through a more complicated method of polynomials [2]. No better result can be attained for the class of all symmetric Boolean functions as Beals et al. provide O($\sqrt{{N}}$) oracle query algorithms to compute the symmetric functions AND and OR [2]. Our success here leads us to apply the results of Chapter 2 to graph properties, which are very well studied in the classical oracle query model, in Chapter 3. While graph properties are not necessarily ``symmetric'' in the sense of Definition 2.5.1, they do display a kind of symmetry.