Our initial state
![]() = (1/
= (1/![]() , 1/
, 1/![]() ,..., 1/
,..., 1/![]() ), is attained by performing the Walsh-Hadamard
transformation on the register in the zero state.
), is attained by performing the Walsh-Hadamard
transformation on the register in the zero state.
Let (k, l ) denote denote the state of our vector, where k is the amplitude of the marked state, and l is the amplitude of each of the remaining (N - 1) states. It is the case in Grover's algorithm that the unmarked states always have the same amplitude, so we can use this shorthand.
After the first application of the Walsh-Hadamard operator to place us
in an equal superposition of states let us say we are in state
![]() = (k0, l0).
= (k0, l0).
From theorem 1 we see the j'th iteration will produce the state
![]() = (kj, lj), where
k0 = l0 = 1/
= (kj, lj), where
k0 = l0 = 1/![]() ,
further:
,
further:
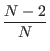 kj +
kj + 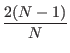 lj
lj
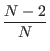 lj -
lj -
With a little work on the recurrence relation we an solve for closed
form solutions of k and j. Let the angle ![]() be defined so
that
sin2
be defined so
that
sin2![]() = 1/N. It can be shown through mathematical
induction that:
= 1/N. It can be shown through mathematical
induction that:
We are interested in the number of iterations for k to have near
unit probability. Evidently, we will find the register to be in the
target state with unit probability when
(2m + 1)![]() =
= ![]() /2, or
when
m = (
/2, or
when
m = (![]() -2
-2![]() )/4
)/4![]() . We can only perform an integer
number of iterations, but the probability of failure is less than
1/N if we iterate
. We can only perform an integer
number of iterations, but the probability of failure is less than
1/N if we iterate
![]()
![]() /4
/4![]()
![]() times, which is
very close to
times, which is
very close to
![]()
![]() when N is large (
1/
when N is large (
1/![]() = sin
= sin![]()
![]()
![]() ). [BBHT96] For the 50 percent
probability called for by Grover's algorithm we need only
). [BBHT96] For the 50 percent
probability called for by Grover's algorithm we need only
![]()
![]() iterations. [BBHT96]
iterations. [BBHT96]