The Quantum Memory Register

Up till now we have considered a two state quantum system, specifically a spin-1/2 particle. However a quantum system is by no means constrained to be a two state system. Much of the above discussion for a 2 state quantum system is applicable to a general n state quantum system.

In an n state system the Hilbert Space has n perpendicular axes, or eigenstates, which represent the possible states that the system can be measured in. As with the two state system, when we measure the n state quantum system, we will always find it to be in exactly one of the n states, and not a superposition of the n states. The system is still allowed to exist in any superposition of the n states while it is not being measured.

Mathematically if two state quantum system with coordinate axes x₀, x₁ can be fully described by:

| X > = w₀*| x₀ > + w₁*| x₁ > = = (w₀, w₁)

Then an n state quantum system with coordinate axes x₀, x₁,..., x_n-1 can be fully described by:

| X > = $$\sum_{{k = 0}}^{{n-1}}$$w_k*| x_k >

In general a quantum system with n base states can be represented by the n complex numbers w₀ to w_n-1. When this is done the state may be written as:

| X > = $$\left(\vphantom{ \begin{array}{c} w_{0} \\ w_{1} \\ \vdots \\ w_{n-1} \end{array} }\right.$$$$\begin{array}{c} w_{0} \\ w_{1} \\ \vdots \\ w_{n-1} \end{array}$$$$\left.\vphantom{ \begin{array}{c} w_{0} \\ w_{1} \\ \vdots \\ w_{n-1} \end{array} }\right)$$

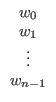
Where it is understood that w_k refers to the complex weighting factor for the k'th eigenstate.

Using this information we can construct a quantum memory register out of the qubits described in the previous section. Note that in general a quantum register composed of n qubits requires 2ⁿ complex numbers to completely describe its state. A n qubit register can be measured to be in one of 2ⁿ states, and each state requires one complex number to represent the projection of that total state onto that state. In contrast a classical register composed of n bits requires only n integers to fully describe its state.

This means that one can store an exponential amount of information in a quantum register relative to the number of qubits it contains. Here we see some of the first hints that a quantum computer can potentially be exponentially more efficient than a classical computer in some respects.