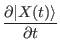Probability Interpretation

Now that we know how to represent our state vector as a superposition of states, and we know that we can only measure the state vector to be in one of the base states, it would seem that there would be some sort of discrepancy. We must determine what happens when we measure the state vector. We know from quantum physics that given an initial condition the state vector will evolve in time in accordance with Schrödenger's equation:

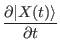ih$${\frac{{\partial \vert X(t) \rangle }}{{\partial t}}}$$ = H(t)| X(t)$$\rangle$$

Where i is the square root of negative one, h is 1.0545*10^-34 Js, and H is the Hamiltonian operator, which is determined by the physical characteristics of the system being evolved.

In our notation this expression is:

ih$${\frac{{\partial w_{i}(t)}}{{\partial t}}}$$ = $$\sum_{{j}}^{}$$H(t)_ij*w_j(t)

This evolution would appear to be continuous, but these equations only apply to a quantum mechanical system evolving in isolation from the environment. The only way to observe the state of the state vector is to in some way cause the quantum mechanical system to interact with the environment. When the state vector is observed it makes a sudden discontinuous jump to one of the eigenstates, but this is not a violation of Schrödenger's equation. When the quantum mechanical system interacts with the outside environment and measured the state vector is said to have collapsed. (Williams, Clearwater)

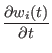Now understanding that a state vector will collapse when it interacts with the external environment, we still need to know in what manner this collapse happens. To perform any sort of useful calculation we must be able so say something about which base state a quantum mechanical system will collapse into. The probability that the state vector will collapse into the j'th eigenstate, is given by | w_j|² which is defined to be a_j² + b_j² if w_j = a_j + i*b_j, where w_j is the complex projection of the state vector onto the j'th eigenstate. In general the chance of choosing any given state is

Prob(j) = $${\frac{{\vert w_{j}\vert^{2}}}{{\sum_{k = 0}^{ n-1} \vert w_{k}\vert^{2}}}}$$

but as mentioned earlier we will insist on having the state vector of length one, and in this case the probability expression simplifies to Prob(j) = | w_j|².

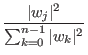
So now we know how to construct an n state quantum system, which can be placed in an arbitrary superposition of states. We also know how to measure the resultant superposition and get a base state with a certain probability. This is all that we need to understand about our quantum memory register to be able to simulate its behavior.